Aerodynamics has recently emerged as a central focus in cycling. From aero socks, reverse mullet wheelsets, aero tires and seemingly everything in between, aerodynamics has taken center stage in the industry. This trend isn’t surprising. At higher speeds, air resistance is 80-90% of the resistive force a rider will encounter on the bike. Aerodynamics can be confusing, unintuitive and hard to quantify, but understanding some of the physics at play can help you ride faster with less effort. In this article, we take a simplified look at the forces acting on cyclists, why aerodynamics plays such a big role in the sport and why it matters to you.

Forces acting on a cyclist

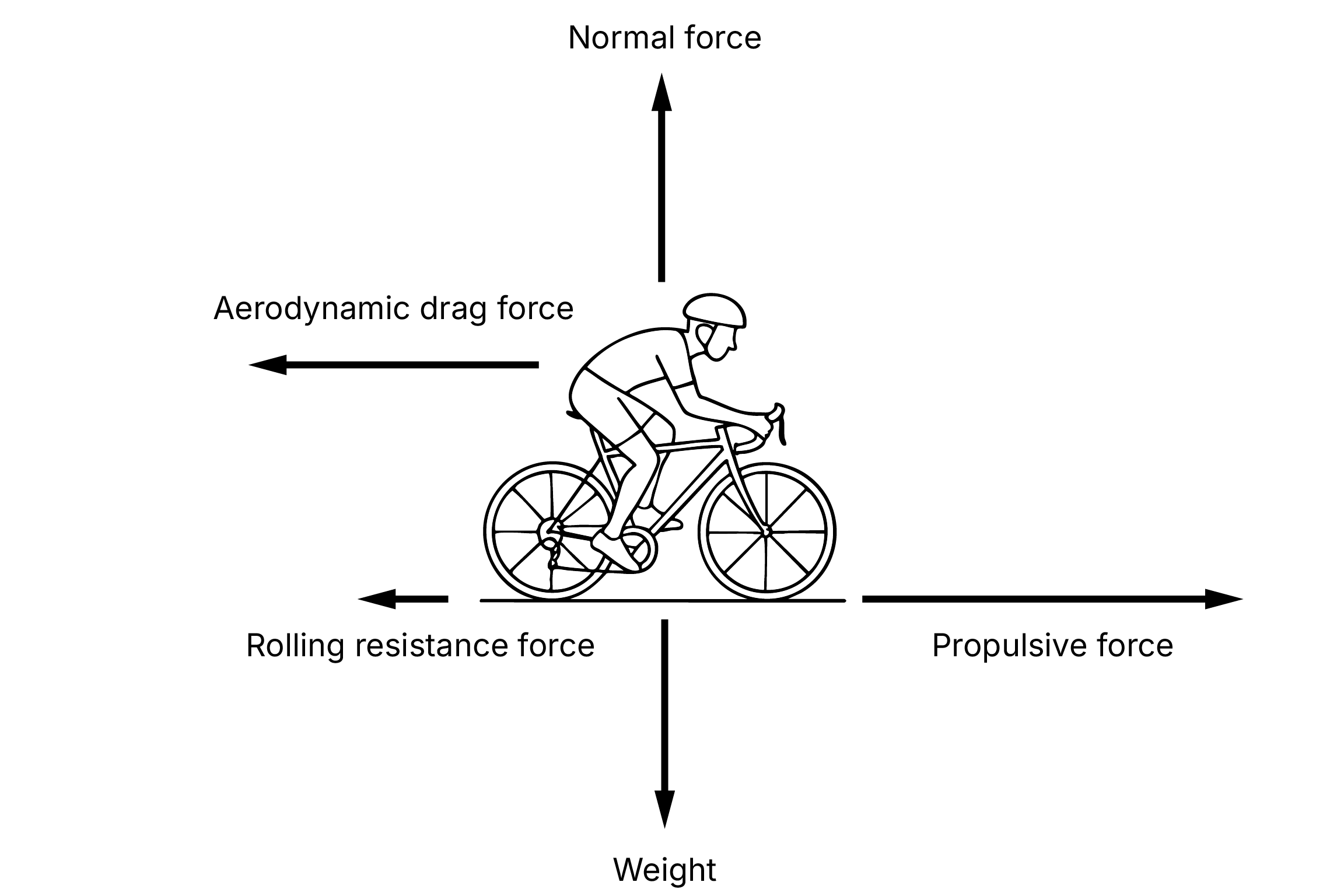
Remember Newtons first law? An object in motion stays in motion unless acted upon by an external force. If a cyclist is traveling at a constant speed in a straight line, the net force in the direction of motion must be zero. This does not mean that there are no forces acting, it means the sum of all the forces equals zero because they balance each other. Let’s take a simplified look at the forces acting on a cyclist traveling at constant speed on a perfectly straight and level road:

Weight ($W$)
Normal force ($N$)
Propulsive force, rider power ($F_p$)
Rolling resistance ($F_{rr}$)
Aerodynamic drag ($F_d$)

From here, we can create a drawing called a free body diagram which shows the forces acting on the cyclist:

Let’s break these forces into vertical and horizontal components:

Vertical forces

We won’t go into too much detail here. The vertical forces consist of weight, W and the normal force, N. Weight is the rider mass times the acceleration due to gravity (9.81 m/s²*). The normal force is a force exerted by a surface (i.e. the road) that is perpendicular to that surface, preventing an object from passing through it. Note that since weight is acting in the downward direction, we assign it a negative value. The normal force will be equal, but opposite and the sum of our vertical forces equals 0. ✅

$$ \sum F_{vertical} =W + N = 0 $$

*This is a metric household, don’t @ me. But if you’re curious, g in freedom units is 32.2 ft/s². 🇺🇸

Horizontal forces

This is what we’re most interested in. The propulsive force $F_p$ is generated by the cyclist pedaling. It is opposed by aerodynamic drag $F_d$ and rolling resistance $F_{rr}$. As with the vertical forces must also be equal to zero in our steady-state (no acceleration) scenario.

$$ \sum F_{horizontal} = F_p + F_{rr} + F_d = 0 $$

Propulsive force

We won’t get too into the weeds with the propulsive force $F_p$ as this is largely understood by cyclists. Dealing with things such as drivetrain losses, whether or not to wax your chain (you should) or using oversized pulley wheels (who are we to tell you how to spend your money?) is beyond the scope of this article. Just know that we’re dealing with forces in this equation and not power. You can calculate $F_p$ by taking rider power (P) and dividing by velocity (v).

$$ F_p=\frac{P}{v} $$

Rolling resistance force

Rolling resistance is the friction between your tires and the road. The force is expressed as:

$$ F_{rr}=C_{rr} \times m \times g $$

where:

$C_{rr}$ = coefficient of rolling resistance (any bicyclerollingresistance.com fans?)

$m$ = mass of bike and rider (kg)

$g$ = gravitational constant (9.81 m/s²)

While $C_{rr}$ changes slightly with velocity, this is often treated as a constant. And because the system mass $m$ and gravitational constant $g$ do not change, $F_{rr}$ can be treated as a constant in our example as well.

Aerodynamic drag force

With all of that out of the way, we’ve made it to the fun part: aerodynamic drag forces, $F_d$.

$$ F_d=\frac{1}{2} \rho v^2C_dA $$

where:

$\rho$ = air density (approximately 1.2 kg/m³ at sea level).

The less dense the air, the lower the drag. Air density is affected by atmospheric pressure, temperature and humidity. Low pressure systems, heat and high humidity (counterintuitively, water is less dense than the nitrogen and oxygen molecules they displace) all reduce the air density. In addition, as altitude increases, air density decreases. This is why you will see riders attempt to break hour records on velodromes at altitude. Filippo Ganna’s 2022 hour record took place at the Tissot Velodrome in Switzerland which sits 450m (1,500 ft) above sea level. While this isn’t as high as Aguascalientes in Mexico (1,887m or 6,200 ft), it offers reduced air density without a large reduction in oxygen partial pressure which can negatively impact rider performance.

$v$ = velocity (m/s)

Take note of the exponent attached to velocity in the equation. More on this later. It is also important to note that the velocity shown here is the speed of the cyclist relative to the air. In our example, we assume zero wind and therefore the air speed is equal to the ground speed. But know that the speed here is not necessarily the speed that you will see on your head unit. This is why drafting and tailwinds help so much in cycling.

👆 The first half of this equation that we’ve discussed so far is what’s known as the dynamic pressure:

$$ P_{dynamic} = \frac{1}{2} \rho v^2 $$

Now, the really important part, CdA:

$C_d$ = coefficient of drag

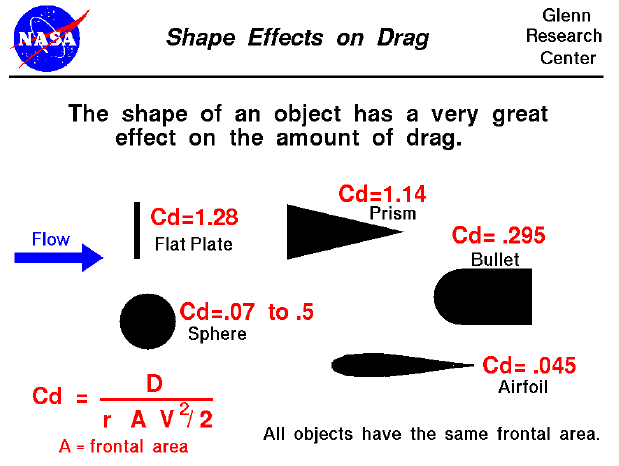
A coefficient is a dimensionless number. In our case, the coefficient of drag helps describe how a force or other aerodynamic quantity relates to the size, speed and shape of an object moving through the air. The drag coefficient is comprised of both pressure (form) drag and skin friction drag which will be discussed in detail in a future article. Cd tells us how “clean” or “draggy” the shape is, irrespective of its size or speed. While large changes in either of these can result in changes to the underlying coefficient, for the sake of simplicity we can assume that they are constant. The image below demonstrates just how big of an impact the shape of an object can have on its drag coefficient. If you’re wondering how a sphere can have such a wild range of Cd values, it’s something we’ll cover in a future article too.

$A$ = frontal area (m²)

The frontal area is the projected area of an object as seen from the direction of the airflow. It is the area that “sees” the wind. In our example where we assume zero wind, the entirety of the airflow hits the cyclist head-on. In the 1980s, Greg LeMond famously used a DIY method to estimate his frontal area. He reportedly cut out photos of himself in his racing position to get an idea of how much area he presented to the wind. LeMond won the 1989 Tour de France by a mere 8 seconds after winning the final time trial by 58 seconds. Crafting pays off.

CdA

In cycling, we typically combine the coefficient of drag and the area into a single quantity, CdA. While drag is a force, CdA is a number modeling that force. CdA helps quantify your total aerodynamic drag and provides a more complete picture of just how “aero” you are. Combining the coefficient of drag along with the frontal area helps better compare riders across a range of riding positions, body types and equipment choices. The ultimate goal is to reduce both the drag coefficient and the frontal area – a small, flat plate (Cd=1.28) can have a lower CdA than a large streamlined airfoil (Cd=0.045). Making yourself smaller and more streamlined is the key to cutting through the air more effectively. Typical CdA values for cyclists range from 0.5 to 0.18 or less for incredibly optimized individuals. These CdA values can be determined experimentally through aerodynamic testing.

🤓 While CdA is often expressed as a dimensionless number, this is technically not correct as it has units of meters squared. Don’t worry, we’re not that pedantic – we’ll omit the units like everyone else.

Double (triple?) trouble

Recall that pesky exponent attached to the velocity in the drag equation? It’s the reason riding fast is hard. While the rolling resistance force remains roughly constant with speed, aerodynamic drag force increases with the square of speed. If you want to double your speed on the bike, you will need to overcome four times the drag force – you’re passing through twice as many air molecules and hitting each molecule with twice the force. But the fun doesn’t stop there. The power required to overcome aerodynamic drag is force times velocity, which means the velocity in the equation is now cubed. To go double your speed, it requires eight times the power. Aren’t exponents fun?

$$ P_{aero}=F_d \times v=\frac{1}{2} \rho v^3C_dA $$

Putting it all together

We learned earlier that a rider must produce enough power to overcome the power lost from aerodynamics and rolling resistance (the sum of all forces are equal to zero). As an example, let’s look a cyclist traveling at 20 km/h (12.4 mph, 5.56 meters per second) and see what it takes to double their speed. We’ll assume the rider is riding upright on the tops with a CdA of 0.4 and an air density of 1.225 kg/m³.

$$ P_{aero}=\frac{1}{2} \times1.225kg/m^3\times(5.56m/s)^3\times0.4=42W $$

Assuming a system mass (rider + bike + gear) of 77kg and a $C_{rr}$ of 0.005, we can then calculate the total power (force times velocity) required at this speed:

$$ P_{rolling}=F_{rr} \times v = 0.005 \times 77kg \times 9.81m/s^2 \times 5.56m/s=21W $$

$$ P_{total}=P_{aero}+P_{rolling}=42W+21W=63W $$

63W. Easy enough. Now, let’s assume everything else remains the same and double the speed to a race pace of 40 km/h (24.8 mph):

$$ P_{aero}=\frac{1}{2} \times1.225kg/m^3\times(11.11m/s)^3\times0.4=336W $$

$$ P_{rolling}= 0.005 \times 77kg \times 9.81m/s^2 \times 11.11m/s=42W $$

$$ P_{total}=P_{aero}+P_{rolling}=336W+42W=378W $$

Power required for a given speed (CdA = 0.40, mass = 77kg, Crr = 0.005)

I don’t know about you, but this number is a big problem. Maybe not if you’re in the world tour, but for us mere mortals, 378 watts is a lot of watts. A massive 89% of the power required here is overcoming aerodynamic drag. Here’s the thing; if you can reduce your CdA to 0.30 by riding on the hoods, the total power required drops to 294W. With a world-class CdA of 0.18, total power decreases even further to a mere 193W.

More with less

You can start to see how aerodynamics plays a critical role in determining your speed on the bike. While raising your FTP by nearly 100W is simply not possible for most of us, training how to ride in an aerodynamic position can allow you to go just as fast on fewer watts. Because the rider accounts for the majority of the total aerodynamic drag, subtle changes in body position can result in big gains. Best of all, changes to your position are free. While there is some truth to being able to “buy speed” by purchasing the latest and greatest aero gear, the reality is that aerodynamics operates on a systems level. Interactions between the rider and equipment all need to be taken into account to ensure the changes being made result in realized gains. The only way to definitively know if something is faster is to perform aero testing. We’ll discuss the different types of aero testing and the pros and cons of each in the next article.

Whether you’re a competitive cyclist or a recreational rider, aerodynamics is by far the biggest barrier to going faster on the bike. If you’re looking to improve your performance, understanding aerodynamics can help you go faster and farther on less effort. Small changes can have a big impact.

Inside Line Engineering is here to help you get faster on the bike. Contact us today to schedule a test and follow us on social media for the latest in aero testing in the Pacific Northwest.

Aerodynamics in cycling